Стандартизация
Непосредственное использование переменных в анализе может привести к тому, что классификацию будут определять переменные, имеющие наибольший разброс значений. Поэтому применяются следующие виды стандартизации:
- Z-шкалы (Z-Scores). Из значений переменных вычитается их среднее, и эти значения делятся на стандартное отклонение.
- Разброс от -1 до 1. Линейным преобразованием переменных добиваются разброса значений от -1 до 1.
- Разброс от 0 до 1. Линейным преобразованием переменных добиваются разброса значений от 0 до 1.
- Максимум 1. Значения переменных делятся на их максимум.
- Среднее 1. Значения переменных делятся на их среднее.
- Стандартное отклонение 1. Значения переменных делятся на стандартное отклонение.
- Кроме того, возможны преобразования самих расстояний, в частности, можно расстояния заменить их абсолютными значениями, это актуально для коэффициентов корреляции. Можно также все расстояния преобразовать так, чтобы они изменялись от 0 до 1.
Таким образом, работа с кластерным анализом может превратиться в увлекательную игру, связанную с подбором метода агрегирования, расстояния и стандартизации переменных с целью получения наиболее интерпретируемого результата. Желательно только, чтобы это не стало самоцелью и исследователь получил действительно необходимые содержательные сведения о структуре данных.
Процесс агрегирования данных может быть представлен графически деревом объединения кластеров (Dendrogramm) либо "сосульковой" диаграммой (Icicle).

Рис. 5.2. Дендрограмма классификации Но подробнее о процессе кластеризации можно узнать по протоколу объединения кластеров (Schedule).
Пример иерархического кластерного анализа. Проведем кластерный анализ по полученным нами ранее факторам на агрегированном файле Курильского опроса:
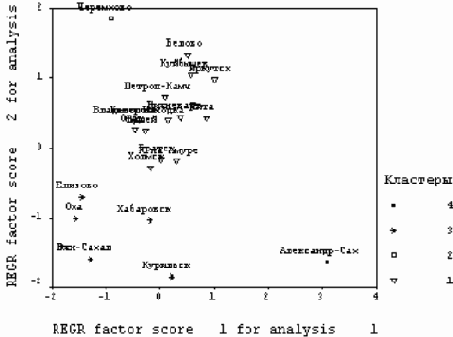
Рис. 5.3. Классификация городов
CLUSTER fac1_1 fac2_1 /METHOD BAVERAGE /MEASURE= SEUCLID /ID=name /PRINT SCHEDULE CLUSTER(3,5) /PLOT DENDROGRAM .
В команде указаны переменные fac1_1 fac2_1 для кластеризации. По умолчанию расстояние между кластерами определяется по среднему расстоянию между объектами (METHOD BAVERAGE), а расстояние между объектами — как квадрат евклидова (MEASURE= SEUCLID).
Кроме того, распечатывается протокол (PRINT SCHEDULE), в качестве переменных выводятся классификации из 3, 4, 5 кластеров (CLUSTER(3,5)) и строится дендрограмма (PLOT DENDROGRAM).
Разрез дерева агрегирования (рис. 5.2) вертикальной чертой на четыре части дал два кластера, состоящих из уникальных по своим характеристикам городов Александровск-Сахалинский и Черемхово; кластер из 5 городов (Оха, Елизово, Южно-Сахалинск, Хабаровск, Курильск); еще один кластер из 14 городов составили последний кластер.
Естественность такой классификации демонстрирует полученное поле рассеяния данных (рис.5.3).
| 1 | 5 | 20 | 0.0115 | 0 | 0 | 2 |
| 2 | 5 | 11 | 0.0175 | 1 | 0 | 3 |
| 3 | 5 | 19 | 0.0464 | 2 | 0 | 11 |
| 4 | 6 | 12 | 0.0510 | 0 | 0 | 8 |
| 5 | 3 | 16 | 0.0549 | 0 | 0 | 9 |
| 6 | 13 | 21 | 0.0808 | 0 | 0 | 10 |
| 7 | 10 | 14 | 0.1082 | 0 | 0 | 14 |
| 8 | 6 | 15 | 0.1349 | 4 | 0 | 11 |
| 9 | 3 | 8 | 0.1538 | 5 | 0 | 13 |
| 10 | 1 | 13 | 0.2818 | 0 | 6 | 12 |
| 11 | 5 | 6 | 0.4560 | 3 | 8 | 13 |
| 12 | 1 | 2 | 0.5768 | 10 | 0 | 16 |
| 13 | 3 | 5 | 0.5861 | 9 | 11 | 16 |
| 14 | 10 | 17 | 0.6130 | 7 | 0 | 17 |
| 15 | 7 | 18 | 0.8098 | 0 | 0 | 17 |
| 16 | 1 | 3 | 1.5406 | 12 | 13 | 18 |
| 17 | 7 | 10 | 2.5726 | 15 | 14 | 19 |
| 18 | 1 | 4 | 3.5613 | 16 | 0 | 19 |
| 19 | 1 | 7 | 5.2217 | 18 | 17 | 20 |
| 20 | 1 | 9 | 14.9146 | 19 | 0 | 0 |
На практике интерпретация кластеров требует достаточно серьезной работы, изучения разнообразных характеристик объектов для точного описания типов объектов, которые составляют тот или иной класс.