БЛОК 4: Моделирование роста числовой последовательности в таблице
Моделирование в таблице роста числовой последовательности
Проработав задания этого блока на персональном компьютере, вы:
Рост ценности денег во времени при начислении сложных процентов подчиняется геометрическому закону, а правило простых процентов производит арифметическую прогрессию. Пользователю электронных таблиц Excel предоставляется избыточное число способов организации вычислений значений элементов этих числовых последовательностей.
Простейшим способом получения арифметической прогрессии в блоке клеток таблицы является операция автозаполнения с помощью мыши, источником данных, для которого служит выделение в таблице двух смежных клеток, содержащих значения двух последовательных членов прогрессии.
Разность арифметической прогрессии при этом вычисляется автоматически и используется программой как постоянный шаг для заполнения блока числовыми константами. Знак шага прогрессии определяется по направлению движения мыши: от меньшего числа в сторону большего – шаг положительный, то есть рост, а от большего к меньшему – снижение. Этот способ обычно применяется для быстрого получения последовательности порядковых номеров.
|
Задание Постройте таблицу порядковых номеров дней високосного года по образцу табл. 2. Сколько дней между датами 23/02 и 08/03? |
Геометрическую прогрессию при помощи автозаполнения получить в Excel нельзя, но она является одним из типов числовой последовательности, которыми можно заполнить блок клеток и без ввода в таблицу явных формул, если использовать команду Правка Заполнить Прогрессия...
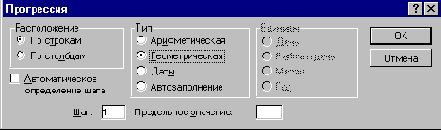
Рис. 26. Диалоговое окно команды Правка Заполнить Прогрессия...
|
Задание Постройте таблицу порядковых номеров дней марта месяца невисокосного года, заполнив вертикальный блок клеток значениями арифметической прогрессии. Чему равен первый член этой прогрессии? |
Правила начисления процентов также могут быть выражены рекуррентно. Рассмотрим динамику роста денежного вклада при простых, и при сложных процентах. Выбор варианта рекуррентной формулы, с помощью которой можно представить правило начисления процентов, дающее в результате одну и ту же числовую последовательность (см. рис. 28), зависит от навыков пользователя Excel, глубины его абстрактного мышления, и потребностей решаемой задачи. Обзор простейших альтернатив организации вычислений приводится в табл. 10.
Таблица 10
Варианты рекуррентного кодирования правил начисления процентов
|
Рост по правилу |
||
|
Процентная ставка выражена |
простых процентов |
сложных процентов |
|
числовой константой 0,15 |
=C3+0,15*C$3 |
=D3+0,15*D3 или =1,15*D3 |
|
абсолютной ссылкой B$1 |
=C3+B$1*C$3 |
=D3+B$1*D3 |
|
именем ячейки ставка |
=C3+ставка*C$3 |
=(1+ставка)*D3 |
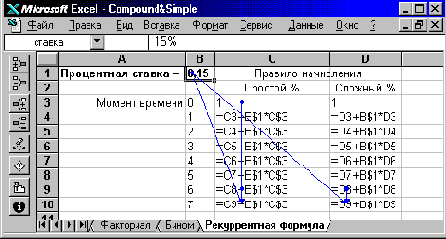
Рис. 27. Модели роста стоимости вклада.
Пример расположения данных на рабочем листе и кодирования необходимых вычислений приведен на рис. 27 в режиме вывода формул. Найденные по этим формулам числовые значения даны на рис. 28.
При использовании рекуррентных формул в процентных вычислениях номера периодов в явном виде в расчете не участвуют, а выполняют в таблице только роль поясняющих надписей. Номер процентного периода (и соответствующего члена прогресии) станет влияющим параметром при другом подходе – расчете на основе общей формулы члена прогресии.
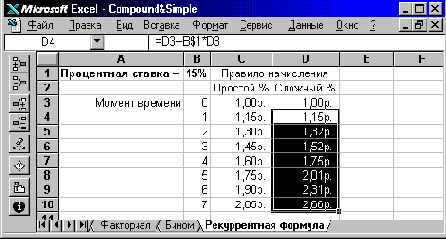
Рис. 28. Числовые значения формул, предложенных на рис. 27.
Пример. Текущая стоимость потока будущих затрат.
Текущая стоимость представляет собой дисконтированную сумму будущих затрат. Дисконтирование производится делением на процентный множитель величина которого зависит от числа процентных периодов, разделяющих моменты осуществления затрат и текущей оценки. Каждый следующий процентный множитель легко рекуррентно получать из предыдущего умножением на знаменатель геометрической прогрессии (1+R), где ставка за один период R=10%.
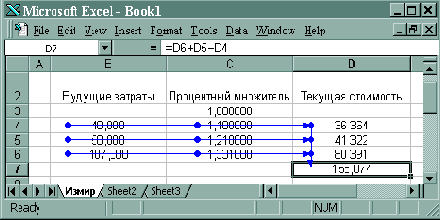
Рис. 29. Рекуррентная модель вычисления текущей стоимости потока будущих платежей.
|
Задание Используя данные рис. 30 и рис. 24 как образец расчета средней ставки простых процентов, взвешенной по периодам действия, найдите среднее значение ставки рефинансирования ЦБ РФ за указанный период. |
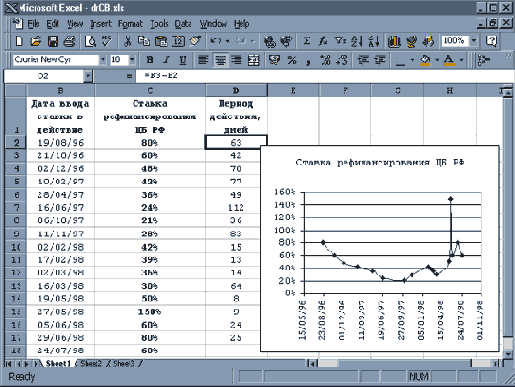
Рис. 30. Динамика ставки рефинансирования ЦБ РФ в 1996–1998 гг.
Пример. Зависимость срока удвоения вклада при начислении сложных процентов от ставки.
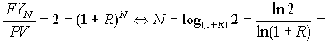
Известен следующий упрощенный способ вычисления срока удвоения вклада при начислении сложных процентов по постоянной ставке R: число 72 делится на число сотых долей в процентной ставке и получается срок удвоения ("правило 72").
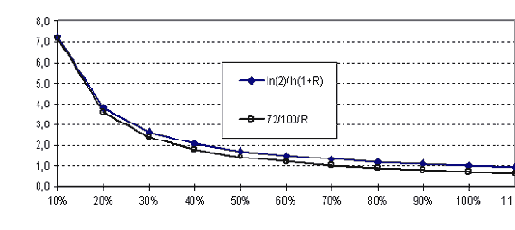
Рис.31. Сравнение точной формулы срока удвоения вклада по сложным процентам и "правила 72".
Действительно (см. рис. 31), при малых R эта функция хорошо аппроксимирует искомую логарифмическую, тем более, что получаемое значение срока обычно нужно округлять вверх до целого числа.
Пример. Последовательность чисел Фибоначчи6 задается двумя своими первыми членами, равными единице, и правилом: каждое новое число равно сумме двух предыдущих.
Для получения в строке электронной таблицы начала последовательности чисел Фибоначчи достаточно задать в отдельных клетках два первых единичных значения, закодировать их адресами формулу, и скопировать ее направо – см. рис. 32.
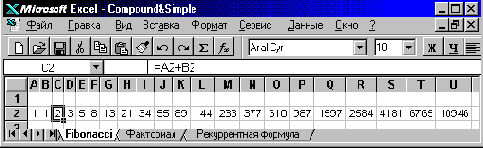
Рис. 32. Табличная формула, моделирующая последовательность чисел Фибоначчи.
Пример . Число возможных перестановок из N элементов равно произведению всех натуральных чисел от 1 до N. Это произведение называется N-факториал и обозначается N! = 1*2*...*N.
По определению, 1!=1. Затем верно рекуррентное правило (N + 1)! = (N + 1) * N!
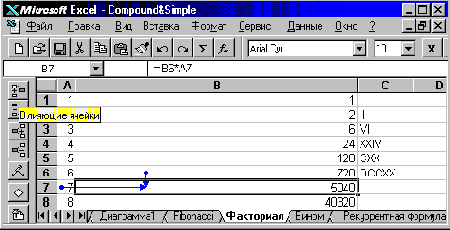
Рис. 33. Рекуррентная табличная модель расчета N!
Пример. Инвестор вносит сумму 5 млн руб на счет с начислением сложных процентов по ставке 8% за период., и затем дважды в конце каждого расчетного периода добавляет на счет столько же.
Какую сумму удастся таким образом нарастить за 3 периода?
Таблица 11
Будущая стоимость потока платежей (млн руб.)
|
Период |
Сумма вклада с процентами в конце периода |
Новый платеж в конце периода |
Переходящий остаток на счете в конце периода |
|
1 |
0,000 = 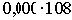 |
5,000 |
5,000 = 0,000 + 5,000 |
|
2 |
5,400 = 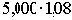 |
5,000 |
10,400 = 5,400 + 5,000 |
|
3 |
11,232 = 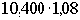 |
5,000 |
16,232 = 11,232 + 5,000 |
При какой процентной ставке те же три платежа по 5 млн руб. каждый, регулярно вносимые на счет в конце периода, позволят накопить сумму не 16,232 млн руб., а 20,000 млн руб.? Чтобы ответить на этот вопрос нужно составить уравнение
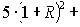
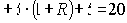
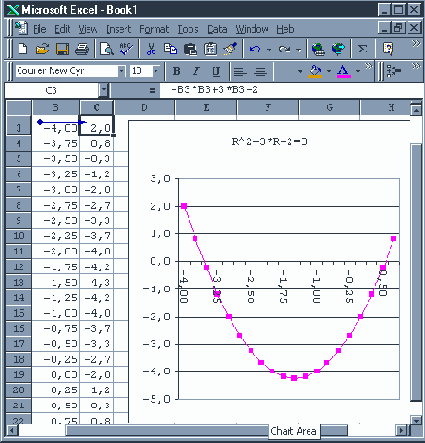
Рис. 34. График левой части квадратного уравнения.
В данном примере уравнение является квадратным (см. рис. 34) и имеет два решения. Значение искомой ставки процентов доставляет положительный правый корень.
Если многочлен в левой части такого уравнения имеет высокий порядок N (число элементов потока платежей), то решений может быть несколько, а единой формулы для нахождения корней не существует. Поэтому ставку подбирают итеративно. Подбор нулевого значения левой части дает ответ R = 56,16%.
Пользователю Excel для нахождения этого ответа достаточно вызвать процедуру Сервис, Подбор Параметра (см. рис. 35). Как хорошо видно на рис. 34, правый корень находится между значениями 0,50 и 0,75. В свободную клетку таблицы, например B24, помещаем начальное приближение 0,60.
В соседнюю клетку C24 вводим формулу левой части уравнения, где место неизвестной ставки R занимает ссылка на влияющую клетку B24. Процедура Подбор Параметра (Goal Seek) итеративным подбором установит (Set cell) в зависимой ячейке (клетка C24 с расчетной формулой левой части уравнения) искомое значение (To value) 0, изменяя значение (By changing cell) влияющей ячейки (клетка B24).
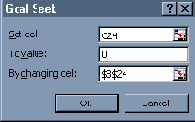
Рис.35. Диалоговое окно процедуры Подбор параметра в оригинальной версии Excel.
Если организовать вычисления не по рекуррентной, а по общей формуле члена прогрессии, то именно номер члена становится ведущим расчетным параметром, поскольку формульное выражение явно ссылается на номер текущего периода. Значения формул меняются в зависимости от номеров моментов времени, ограничивающих периоды.
В левой части окна на рис.36 использована формула массива (со ссылкой на интервал A2:A9 значений параметра N – срок), а справа – обычная техника копирования формул.
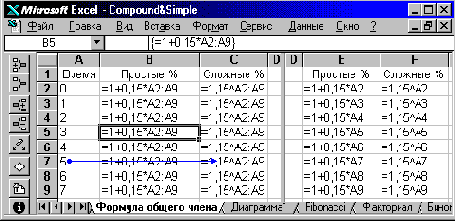
Рис. 36. Модели организации табличных вычислений по общей формуле члена прогрессии.
Дальнейшим развитием идеи организации на рабочем листе блоков данных, табулирующих влияние частного изменения параметра на значение исследуемой функции, является процедура создания таблиц "анализа чувствительности" (англ. What-If Analysis), инициируемая командой Данные, Таблица подстановки...
Правила использования этой процедуры Excel требуют такой записи расчетных формул, чтобы они не содержали ссылок ни на какие внутренние ячейки области создаваемой таблицы, в том числе не ссылались и на клетки с числовыми значениями параметра. Чтобы математические выражения при этом все-таки можно было как-то закодировать, договорились внутри формулы на месте параметра ставить "местоимение" – адрес ячейки ввода.

Рис. 37. Определение таблицы подстановки, данное в Справочной системе Microsoft Excel.
Ячейкой ввода может быть, независимо от содержимого, любая ячейка рабочего листа вне области таблицы подстановки. Попробуем представить два правила начисления процентов как таблицу подстановки "с одной ячейкой ввода", то есть с одним параметром, каковым является в данном случае дискретно заданное время.
До вызова этой процедуры необходимо, чтобы уже был заполнен значениями параметра интервал смежных клеток столбца (в блок B3:B10 записаны номерами периодов от 0 до 7), и на одну строку выше первого значения параметра в столбцах правее располагаются формулы табулируемых функций, ссылающиеся на ячейку ввода..
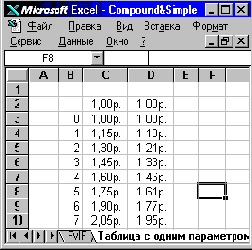 а) режим вывода значений |
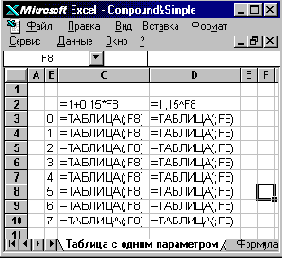 б) режим вывода формул |
Моменты времени занумерованы на рабочем листе вертикально, то есть влияющий параметр меняется по строкам внутри одного столбца. Поэтому адрес выбранной ячейки ввода нужно сообщить во втором поле ввода диалогового окна, оставив первое поле пустым.
Если интервал значений параметра таблицы подстановки на рабочем листе располагается горизонтально, то отвечать необходимо наоборот, только на первый вариант вопроса. Ссылаться на обе ячейки ввода пользователю приходится при построении таблиц подстановки, зависящих от двух параметров.
Пусть, например, ячейкой ввода будет F8. В клетку C2 введем знакомую формулу простых процентов =1+0,15* F8, а в клетку D2 – сложных =1,15^ F8. Далее нужно выделить всю область таблицы подстановки – блок B2:D10 и применить команду Данные Таблица подстановки...
При необходимости изменить расчетную формулу, например поставить 20% вместо 15%, теперь достаточно отредактировать выражение только в формуле верхней строки таблицы подстановки.
Задание Заполните блок клеток рабочего листа электронной таблицы колонками значений и постройте по ним диаграммы роста стоимости одной денежной единицы, вложенной на срок 18 месяцев по ставке 24% годовых при начислении процентов: Постройте искомые таблицы значений будущая стоимость 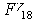 |
Ранее было рассмотрено построение таблицы дисконтирующих множителей PVIF(R,N) для 4% < R < 10% с шагом 1% для N=1, 2, 3 методом копирования формул. Например, в клетку B3 помещается выражение =1/(1+B$2)^$A3, которое кодирует правило построения таблицы: "считаем число, обратное сумме единицы и ставки процента, возведенной в степень, заданной как срок; причем значение процента берем всегда из самой верхней строки, а срок – всегда из крайней левой колонки".
Для поддержания единства блока клеток, заполненного одной формулой, методу копирования формул лучше предпочесть встроенную процедуру Данные Таблица подстановки... и построить с её помощью таблицу-массив с двумя параметрами.
Начинать изготовление таблицы значений множителей наращения, показанной на рис.39, нужно с заполнения части столбца A3:A5 рядом значений срока и части строки B2:H2 последовательностью значений ставки сложных процентов. После этого в левый верхний угол области будущей таблицы подстановки (ячейка A2) вводится расчетная формула, в которой в роли ссылок на параметры выступают адреса двух ячеек ввода, внешних по отношению к области таблицы. В качестве ячейки, куда будет подставляться процентная ставка, выбрана A1, а ссылка на срок заменяется обращением к ячейке E1. Расчетная формула в клетке A2 имеет вид =(1+A1)^E1. Затем необходимо выделить блок ячеек A2:H5 и дать команду Данные Таблица подстановки...

Рис. 39. Множители наращения сложных процентов FVIF(R,N).
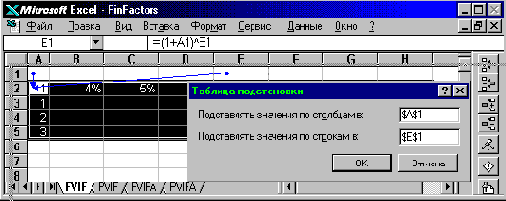
Рис. 40. Построение таблицы данных с двумя параметрами.
В первое поле ввода диалогового окна рис.41, щелчком мыши помещена абсолютная ссылка на ячейку A1, занимающую в производящей формуле таблица параметр R – процентную ставку, значения
которой расположены над таблицей горизонтально, то есть меняются по столбцам внутри одной строки.
Во втором поле ввода нужно дать ссылку на ячейку E1, куда будут подставляться значения параметра N – срок, интервал изменения которого задан слева вертикально, то есть в одном столбце по строкам.
6 Итальянский монах и математик Леонардо из Пизы, более известный под именем Фибоначчи (сын Боначчи). Фибоначчи познакомил Европу с достижениями индийской (арабской) математики. Именно он ввел в обиход арабские цифры и позиционную десятичную систему счисления, чем положил начало эпохи коммерческой арифметики в средние века. См.: Соколов Я.В. Бухгалтерский учет: от истоков до наших дней. М., 1996.
Модуль 3.
Оценка параметров потоков платежей
Оценка параметров потоков платежей
В финансовой практике широко распространены контракты, предусматривающие не разовое, а систематическое движение средств – выплаты/поступления по заданному графику происходят регулярно.
Последовательность платежей, разделенных равными интервалами времени, называется равномерной
финансовой рентой или потоком платежей. Поток платежей одинакового размера называется постоянной финансовой рентой или аннуитетом (англ. annuity). Если платежи неодинаковы по знаку и размеру, то применяется более общий термин денежный поток (от англ. cash flow).
Блок 5 посвящен методике математического дисконтирования денежного потока будущих доходов/расходов инвестиционного проекта и построенным на её основе критериям эффективности капиталовложений.
Блок 6 знакомит читателя с широко применяемым в финансовом анализе понятием аннуитета и возможностями автоматизации стандартных вычислений с использованием встроенных функций Excel.