БЛОК 1: Рост стоимости вложений за счет присоединения процентов

РОСТ СТОИМОСТИ ВЛОЖЕНИЙ ЗА СЧЕТ ПРИСОЕДИНЕНИЯ ПРОЦЕНТОВ

При изучении этого блока вы узнаете, что такое:

процентная и учетная ставка;

обыкновенные и точные проценты;

простые и сложные проценты;

дискретные и непрерывные проценты;

номинальная, эффективная и реальная доходность.

При изложении материала далее используются следующие термины и обозначения:

Процентные деньги (англ. interest money), называемые часто коротко "проценты", представляют собой абсолютный доход от предоставления долга. Этот доход принято исчислять в сотых долях от размера вложенной суммы, то есть в процентах (от лат. pro centum – за сто).

PV – текущая стоимость (англ. present value) – исходная сумма долга или оценка современной величины денежной суммы, поступление которой ожидается в будущем, в пересчете на более ранний момент времени.

FV – будущая стоимость (англ. future value) – сумма долга с начисленными процентами в конце срока.

R – ставка процента (англ. rate of interest) является относительным показателем эффективности вложений (норма доходности), характеризующим темп прироста стоимости за период.

N – срок

погашения долга (англ. number of periods) – интервал времени, по истечении которого сумму долга и проценты нужно вернуть. Срок измеряется числом расчетных периодов – обычно равных по длине подынтервалов времени, в конце которых регулярно начисляются проценты.

Процентная ставка R = (FV – PV) / PV измеряет уровень доходности отнесением абсолютного эффекта (полученного дохода в виде суммы процентных денег, начисленных за весь срок) к исходной сумме долгового обязательства PV. Интересно, что до социалистической революции в России слово "интерес" употреблялось как финансовый термин для обозначения суммы процентного дохода.

Если соотнести сумму процентов (FV – PV) не с PV, а с будущей стоимостью FV, наращенной по мере присоединения процентов, то получится другая мера эффективности – темп снижения D = (FV – PV) / FV, называемый в финансах учетной ставкой (англ. discount rate), или нормой банковского дисконтирования. Дисконтом в данном случае называется скидка в цене при продаже долгового обязательства (ценной бумаги) ниже номинала.

Задание

Выразите процентную ставку R через учетную ставку D, используя соотношение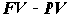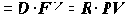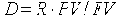

<
Пример. Вы заняли сегодня 4 руб., дав обязательство вернуть к указанной дате 5 руб.

Оценим доходность этой сделки для кредитора показателями нормы процента R и учетной ставки D, приняв весь период между двумя моментами времени за полный срок договора, приняв его за единицу времени N=1.

PV = 4 руб., FV = 5 руб., FV – PV = 5 – 4 = 1 руб., R = 1/4 = 25%, D = 1/5 = 20%.

Пример. Банк привлек денежные средства клиента в сумме 376 000 руб., в обмен на вексель (долговое обязательство) по предъявлении номиналом 509 500 руб., который через 6 дней был погашен.

Процентный доход клиента за 6 дней составляет 509 500 – 376 000 = 133 500 руб.

Процентная ставка за 6 дней 133 500 / 376 000 = 35,51%. За 1 день 35,51% / 6 = 5,9%.

Учетная ставка за 6 дней 133 500 / 509 500 = 26,20%. За 1 день 26,20% / 6 = 4,4%.

Простые проценты начисляются по ставке R на одну и ту же постоянную базу - исходную сумму долга PV, что за счет многократного прибавления постоянной величины процентного дохода за один период

приводит к росту

за полный срок N

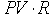
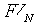
периодов по закону арифметической прогрессии.

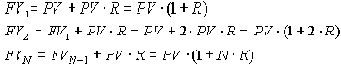
Множитель наращения по правилу простых процентов равен

. Он показывает будущую стоимость одной денежной единицы, вложенной сроком на N периодов при начислении в конце каждого из них процентного дохода по ставке R без капитализации начисленных ранее процентов.

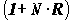
Таблица 1

Наращение и изъятие дохода при начислении простых процентов

Год	Сумма вклада в начале года (руб.)	Будущая стоимость (сумма на счете в конце года) при по ставке R = 15% годовых (руб.)	Процентный доход (снят со счета в конце года) (руб.)	Остаток на счете (руб.)
1	10 000	11 500 = (1+0,15)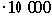	1 500	10 000
2	10 000	11 500 = (1+0,15)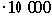	1 500	10 000
3	10 000	11 500 = (1+0,15)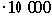	1 500	10 000

Номинальные процентные ставки традиционно объявляются на период, равный одному календарному году N = 1, а срок более короткой финансовой операции измеряется обыкновенной дробью – долей года

, 0 < N

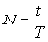
< 1, которую получают как отношение срока операции t к длине целого года. Если учитывается точное число дней в году (T=365 или 366), то говорят о начислении точных процентов. При расчете обыкновенных процентов

год округляется до 360 = 12 месяцев по 30 дней. Срок операции t можно рассматривать точно или приблизительно.

Пример. Денежные средства в сумме 20 тыс.руб. приняты Банком в срочный вклад на 3 месяца.

Найдем будущую стоимость вклада при начислении процентов по ставке R = 29% годовых.

обыкновенные проценты с приближенным числом дней

тыс. руб.

обыкновенные проценты с точным числом дней

тыс. руб.

точные проценты с точным числом дней

тыс. руб.

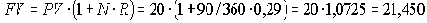
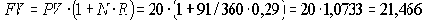
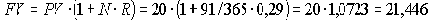
Для точного расчета срока финансовой операции необходимо знать порядковые номера всех дней в году. Тогда срок t

находится как разность номеров дней заключения и окончания договора (в расчет процентов по вкладам добавляется еще один день, то есть полностью включаются все дни срока). Например, если долг образовался сегодня, а погашаться будет завтра, то следующие друг за другом даты отличаются на 1, а срок долгового обязательства, используемый при начислении процентов, при включении в него дат начала и окончания договора составляет 2 дня. При докомпьютерной технологии организации расчетов для ускорения вычислений используют справочную таблицу, подобную табл. 2.

Таблица 2

Порядковые номера дней в невисокосном году

Месяц число	1	2	3	4	5	6	7	8	9	10	11	12

1	1	32	60	91	121	152	182	213	244	274	305	335
2	2	33	61	92	122	153	183	214	245	275	306	336
3	3	34	62	93	123	154	184	215	246	276	307	337
4	4	35	63	94	124	155	185	216	247	277	308	338
5	5	36	64	95	125	156	186	217	248	278	309	339
6	6	37	65	96	126	157	187	218	249	279	310	340
7	7	38	66	97	127	158	188	219	250	280	311	341
8	8	39	67	98	128	159	189	220	251	281	312	342
9	9	40	68	99	129	160	190	221	252	282	313	343
10	10	41	69	100	130	161	191	222	253	283	314	344
11	11	42	70	101	131	162	192	223	254	284	315	345
12	12	43	71	102	132	163	193	224	255	285	316	346
13	13	44	72	103	133	164	194	225	256	286	317	347
14	14	45	73	104	134	165	195	226	257	287	318	348
15	15	46	74	105	135	166	196	227	258	288	319	349
16	16	47	75	106	136	167	197	228	259	289	320	350
17	17	48	76	107	137	168	198	229	260	290	321	351
18	18	49	77	108	138	169	199	230	261	291	322	352
19	19	50	78	109	139	170	200	231	262	292	323	353
20	20	51	79	110	140	171	201	232	263	293	324	354
21	21	52	80	111	141	172	202	233	264	294	325	355
22	22	53	81	112	142	173	203	234	265	295	326	356
23	23	54	82	113	143	174	204	235	266	296	327	357
24	24	55	83	114	144	175	205	236	267	297	328	358
25	25	56	84	115	145	176	206	237	268	298	329	359
26	26	57	85	116	146	177	207	238	269	299	330	360
27	27	58	86	117	147	178	208	239	270	300	331	361
28	28	59	87	118	148	179	209	240	271	301	332	362
29	29		88	119	149	180	210	241	272	302	333	363
30	30		89	120	150	181	211	242	273	303	334	364
31	31		90		151		212	243		304		365

<

Пример. Вы заняли 21 февраля 40 тыс.руб., обязавшись вернуть 23 августа сумму долга с точными простыми процентами по ставке 50% годовых.

По табл. 2 определяем номера дней. 21 февраля – это 52 день года, а 23 августа – 235 по счету день, если год невисокосный. Тогда t = (235 – 52) + 1 = 183 + 1 = 184 дня. 23 августа следует вернуть кредитору сумму

тыс. руб.

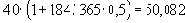
Пример. 27 сентября 2000 года молодая семья разместила временно свободные денежные средства в сумме 40 тыс. руб. во вклад сроком 120 дней по ставке 9% годовых (см. табл. 3), предпочтя этот вариант двум индивидуальным вкладам по 20 тыс. руб. каждый.

Когда заканчивается срок вклада? Дата 27 сентября внутри года имеет порядковый номер 270. До конца года пройдет (365 – 270) + 1 = 96 дней. В 2001 г. вклад пролежит в Банке 120 – 96 = 24 дня. 24 января можно снять сумму срочного вклада с процентами. До момента явки вкладчика за деньгами средства переводятся на счет до востребования.

Множитель наращения по ставке 8% =

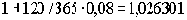
Множитель наращения по ставке 9% =

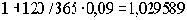
Выигрыш от инвестирования 40 тыс. руб. по более высокой ставке =

= 131 руб. 51 коп.

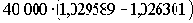
Увеличение процентной ставки при удлинении срока депозита связано с тем, что, доверяя Банку свои сбережения на длительное время, клиенты ожидают получить компенсацию за повышение риска невозврата долга за счет повышения доходности сделки. Графическое представление зависимости доходности вложений от их срока принять называть "кривой доходности"3. Форма кривых доходности, построенных на рис.1 по данным табл. 3 о ставках вкладов в сумме свыше 30 тыс. руб. с начислением процентов в конце срока указывает на то, что в данном случае, привлекая средства на более длительное время, Банк меньше платит за риск, связанный со сроком, чем по более коротким депозитам.

Таблица 3

Ставки по вкладам физических лиц в рублях в Банке "Санкт-Петербург", % годовых

Срок	Порядок начисления процентов	20 марта 2000 года	25 сентября 2000 года
От 15 до 30 тыс. руб.	Свыше 30 тыс. руб.	От 15 до 30 тыс. руб.	Свыше 30 тыс. руб.
31 день	в конце срока	10,0	11,0	4,5	5,0
60 дней	в конце срока	18,0	20,0	5,5	6,0
91 день	ежемесячно	20,5	21,5	7,4	7,9
91 день	в конце срока	21,0	22,0	7,5	8,0
120 дней	ежемесячно	22,0	23,0	7,9	8,9
120 дней	в конце срока	23,0	24,0	8,0	9,0

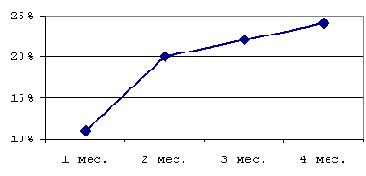
Рис. 1. Кривая доходности.

Пример. Иван Спиридонович сделал 3 августа 1999 г. депозитный вклад в сумме 50 тыс. руб. на срок 365 дней по ставке 36% годовых, а Василий Семенович, ожидая роста процентных ставок по вкладам физических лиц в коммерческих банках, разместил такую же сумму на срок 120 дней, и затем дважды оформлял через 120 дней новый вклад, реинвестируя полностью исходную денежную сумму вместе с начисленными за 4 месяца процентами.

Используя табл. 2, определите дату окончания срока последнего (третьего) вклада Василия Семеновича на 120 дней?

Иван Спиридонович 3 августа 2000 г. может получить

50 тыс. руб., так как снижение Банком процентных ставок не распространяется на ранее заключенные срочные договора. Решение Василия Семёновича привело к такому финансовому результату (см. табл. 4).

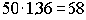
Таблица 4

Реинвестирование вклада под простые проценты

Дата	Процентная ставка	Множитель наращения	Будущая стоимость
03/08/99	34%	1,11333	55,667
01/12/99	32%	1,23209	61,604
30/03/00	24%	1,33066	66,533

В данном случае за 360 дней средняя процентная ставка как годовой темп прироста в данном случае составила (66,533 – 50,000) / 50,000 = 33% годовых.

Ожидаемая вкладчиком выгода реинвестирования процентного дохода не была получена как в результате изменения условий приема вкладов, так и за счет более низкой ставки привлечения средств Банком на короткий срок.

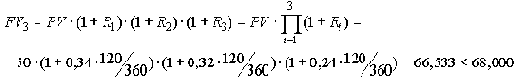
Задание

Оцените результат реинвестирования в условиях данного примера при сохранении процентной ставки по вкладам сроком на 120 дней на постоянном уровне R = 120% годовых.

Реинвестирование процентного дохода по постоянной ставке R является ступенчатым приближением к показательному росту по правилу сложных процентов

, где буквой M обозначено число моментов реинвестирования.

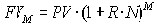
При заключении между должником и кредитором финансового договора на срок, превышающий один расчетный период (N > 1) выбор базы для дальнейшего начисления процентов имеет принципиальное значение. Применение постоянной ставки начисления к постоянной базе дает рост по правилу простых процентов – арифметическую прогрессию с постоянной разностью, равной процентному доходу за период.

В краткосрочных операциях на срок до года (N

< 1) чаще используется правило простых процентов.

Сложные проценты характеризуются тем, что база начисления растет в результате регулярного присоединения к ней процентных денег, причитающихся кредитору за предыдущие расчетные периоды. Получается геометрическая прогрессия с постоянным знаменателем, равным множителю наращения (1 + R) за один период по ставке процентов R.

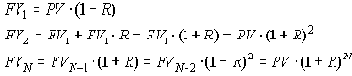
Таблица 5

Наращение и присоединение дохода при начислении сложных процентов

Год	Сумма вклада в начале года (руб.)	Будущая стоимость (сумма в конце года) при по ставке R = 15% годовых (руб.)	Процентный доход (присоединен к сумме вклада в конце года) (руб.)	Остаток на счете (руб.)
1	10 000	11 500 =	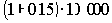1 500	11 500
2	11 500	13 225 =	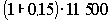1 725	13 225.
3	13 225	15 209 =	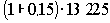1 984	15 209

Множитель наращения сложных процентов за полный срок N периодов по процентной ставке R за каждый

является основным финансовым коэффициентом и показывает будущую стоимость 1 денежной единицы, вложенной на N периодов под сложные проценты, начисляемые в по ставке R.

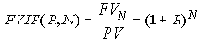
Для обозначения данного финансового коэффициента используется стандартная аббревиатура FVIF (от англ. Future Value Interest Factor – процентный множитель будущей стоимости). Будущая стоимость определяется умножением размера первоначально инвестированной суммы на этот коэффициент

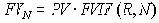
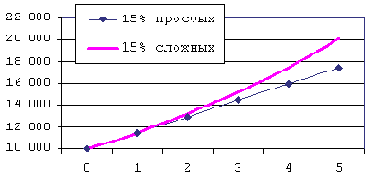
Рис. 2. Рост при начислении простых и сложных процентов по одинаковой ставке R.

Геометрический рост по правилу сложных процентов при N > 1 обгоняет арифметическую прогрессию простых процентов. Так, трижды заработав на вложенные 10 тыс. руб. проценты по 1,5 тыс. руб. в год, вкладчик имеет в конце срока

= 14,5 тыс. руб., тогда как а наращение сложными процентами приносит ему будущую стоимость 15,209 тыс. руб. При удлинении срока вклада эта тенденция усиливается (см. рис. 2).

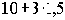
Задание

По какой ставке простых процентов можно за 4 года нарастить сумму, равную будущей стоимости исходной суммы средств за тот же срок при начислении дохода по ставке 15% сложных годовых?

<

Для того, чтобы найти ответ необходимо выразить искомую ставку простых процентов R из условия равенства множителей наращения по простым и сложным процентам:

сложные проценты

простые проценты

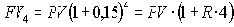
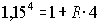
Пример. За два расчетных периода при начислении сложных процентов вклад вырос с PV = 75 руб. до FV2 = 112,5 руб.

Из формулы сложных процентов

выразим ставку R.

.

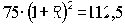
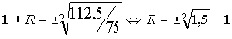
В качестве процентной ставки выбирается тот из двух возможных ответов данной математической задачи, который больше нуля. Так как результатам извлечения корня является иррациональное число (бесконечная дробь), ответ округляется с приемлемой точностью, например, до сотых R = 22,47%.

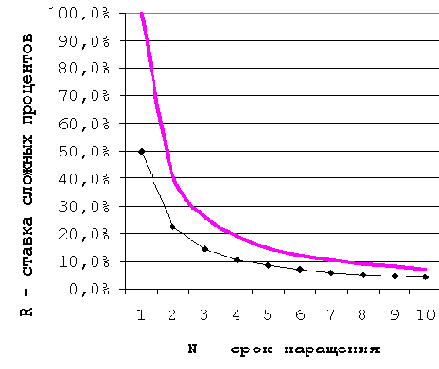
Рис. 3. Зависимость процентной ставки от срока наращения.

По этой ставке за два периода вклад вырастает в полтора раза. Общий вид зависимости ставки сложных процентов R от срока N при фиксированном значении коэффициента наращения

и 2,0 представлен далее на рис. 3. Верхняя кривая соответствует большему значению FVIF(R; N) = 2.

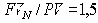
Задание

За какой срок (число процентных периодов) вклад удвоится при начислении простых процентов по ставке R = 30%? Множитель наращения простых процентов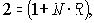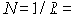

откуда

За какой срок вклад удвоится при начислении сложных процентов по той же ставке?

Отметьте соответствующую точку на рис. 3.

При более частом, чем один раз в год, начислении сложных процентов внутри года, размер номинальной годовой ставки R пропорционально уменьшают (традиция приближенных вычислений восходит к правилу простых процентов), а длину срока в процентных периодах увеличивают во столько же раз. Обозначим внутригодовую частоту начисления сложных процентов буквой m.

В случае ежемесячной капитализации (m

= 12) календарный срок 2 года выражается числом расчетных периодов периодов

месяца, а ежемесячная процентная ставка получается из номинальной годовой делением на 12. Ясно, что при одинаковой номинальной годовой ставке R увеличение частоты начисления сложных процентов m приводит в конце каждого года к большему финансовому результату в виде будущей стоимости FV.

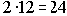
Через N полных лет

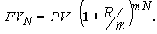
Эффективным годовым процентом называется процентный доход, получаемый инвестором за один год в результате вложения одной денежной единицы по номинальной годовой ставке сложных процентов R при частоте начисления m раз в год.

.

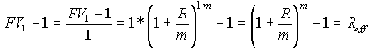
Абсолютная величина эффективного процента, отнесенная к одной целой денежной единице, дает годовую эффективную норму процента.

Эффективная доходность вложений является инструментом приведения условий финансовых контрактов к сопоставимому виду.

Задание

У Вас есть свободная сумма PV = 1000 руб., которую Вы намерены пустить в рост на 12 месяцев под сложные проценты. Куда вы положите свои деньги, если доступные альтернативы таковы:

Банк "Алиса" принимает вклады от населения под 16% годовых, начисляемых ежеквартально.

Банк "Базилио" предлагает 12% годовых при ежемесячном начислении.

Отделение иностранного банка "Carabas" дает 20% годовых, выплачиваемых каждые полгода.

Таблица 6

Сравнение условий приема вкладов по эффективной норме процента

Банк A ("Алиса")	Банк B ("Базилио")	Банк C ("Carabas")
16%	12%	20%	R – номинальная годовая ставка сложных %
4	12	2	m – частота внутригодового начисления %;
4% за квартал	1% в месяц	10% за полгода	ставка %, соответствующая длине внутригодового периода начисления
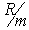1,044 =	1,0112 =	1,12 =	FV – будущая стоимость вклада через 1 год (N = 1)

В современных условиях в связи с развитием систем электронных платежей проценты могут начисляться даже чаще, чем один раз в день. При бесконечно частом (

) дроблении года на малые процентные периоды, то есть при непрерывном наращении сложных процентов получается показательный закон роста

, так как

при

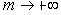
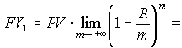
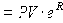
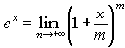
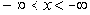
Номинальную годовую процентную ставку R, являющуюся показателем степени в формуле множителя непрерывного наращения, называют интенсивностью, или силой роста. Она связана с годовой эффективной нормой процента

соотношением

. Будущая стоимость после непрерывного начисления сложных процентов за N лет

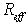
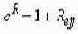
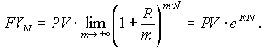
Конечный случай

называют дискретным начислением процентов.

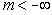
На реальную доходность вложений существенно влияет изменение покупательной способности денег за период, охватываемый финансовой операций. Процесс падения покупательной способности бумажных денег вследствие дополнительной эмиссии или по причине сокращении товарной массы при сохранении неизменного количества денег в обращении называется инфляцией

(от лат. influtio – вздутие). Инфляция проявляется в повышении стоимости жизни и росте цен.

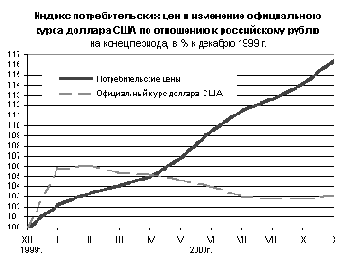
Рис. 4. Сравнительная динамика индекса цен и валютного курса в 2000 г.4

Одним из подходов к измерению реальной покупательной способности фиксированной денежной суммы по прошествии срока N

является соотнесение ее с уровнем инфляции за N периодов. В каждом последующем инфляционном периоде обесцениваются уже ранее обесцененные деньги, поэтому реальная величина будущей стоимости

, независимо от правила начисления процентов, применяемого для ее наращения, находится делением на цепной темп роста

. С учетом инфляции реальная эффективная доходность I определяется по эффективной годовой ставке R и уровню инфляции h из условия

как

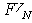
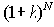
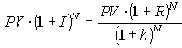
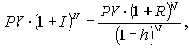
и в странах с низкой инфляцией знаменатель этой дроби в расчетах принимают иногда равным единице.

Уровнем инфляции h называется темп прироста индекса цен5 за выбранный период. Другим методом измерения инфляции, широко использовавшимся в России до 2000 г, является учет колебаний валютного курса (покупательная способность на один товар – иностранную валюту). Как видно выше на рис.4, к концу 2000 г. индекс потребительских цен заметно обогнал курс доллара США, который был стабилизирован и перестал быть индикатором инфляции.

Задание

Какой реальный доход получит вкладчик, разместивший на срок на 1 год сумму 1000 руб. на условиях ежемесячного начисления сложных процентов по номинальной годовой ставке 17% и среднегодовом уровне инфляции 18%? Начните выполнение задания с расчета эффективного годового процента.

Пример. Располагая свободной на полгода суммой 1000 долл. США, предприниматель решил вложить их на срочный вклад и собрал информацию о ставках привлечения Банком на этот срок средств физических лиц в зависимости от вида валюты (см. табл. 7) с начислением простых процентов.

Таблица 7

Депозитные ставки и курсы обмена валют в начале и в конце срока договора

	RUR	USD	DEM
01/12/99 Сумма вклада	26 530	1 000
Обменный курс ЦБ РФ к рублю 01/12/99		26,53	13,66
Депозитная ставка на 180 дней, % годовых	31%	4%	3,5%
29/05/00 Будущая стоимость	30 642	1 020
Обменный курс ЦБ РФ к рублю 01/12/99	1 084	28,27	13,19
Депозитная ставка на 180 дней, % годовых	24%	3%	2,5%

Ожидая укрепления доллара США (не имея достоверного прогноза на 180 дней вперед), вкладчик предпочел внести средства на валютный депозит. Однако, если бы он конвертировал иностранную валюту и оформил свой вклад в российских рублях, результат наращения был бы выше:

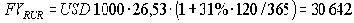
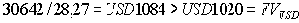
Задание

Оцените величину упущенного инвестором дохода в случае размещения той же суммы на валютный депозит через конверсию в немецкие марки.

Каков эффективный годовой процент по этим валютным вкладам при полугодовом реинвестировании?

3 См.: Четыркин Е.М. Методы финансовых и коммерческих расчетов. М., 1995.

4 Источник: Госкомстат РФ – www.gks.ru

5 Пример расчета индекса цен на корзину продуктов см. далее в блоке 2.

Содержание раздела