Задачи регрессионного анализа
Рассмотрим основные задачи регрессионного анализа: установление формы зависимости, определение функции регрессии, оценка неизвестных значений зависимой переменной.
Установление формы зависимости.
Характер и форма зависимости между переменными могут образовывать следующие разновидности регрессии:
- положительная линейная регрессия (выражается в равномерном росте функции);
- положительная равноускоренно возрастающая регрессия;
- положительная равнозамедленно возрастающая регрессия;
- отрицательная линейная регрессия (выражается в равномерном падении функции);
- отрицательная равноускоренно убывающая регрессия;
- отрицательная равнозамедленно убывающая регрессия.
Однако описанные разновидности обычно встречаются не в чистом виде, а в сочетании друг с другом. В таком случае говорят о комбинированных формах регрессии.
Определение функции регрессии.
Вторая задача сводится к выяснению действия на зависимую переменную главных факторов или причин, при неизменных прочих равных условиях, и при условии исключения воздействия на зависимую переменную случайных элементов. Функция регрессии определяется в виде математического уравнения того или иного типа.
Оценка неизвестных значений зависимой переменной.
Решение этой задачи сводится к решению задачи одного из типов:
- Оценка значений зависимой переменной внутри рассматриваемого интервала исходных данных, т.е. пропущенных значений; при этом решается задача интерполяции.
- Оценка будущих значений зависимой переменной, т.е. нахождение значений вне заданного интервала исходных данных; при этом решается задача экстраполяции.
Обе задачи решаются путем подстановки в уравнение регрессии найденных оценок параметров значений независимых переменных. Результат решения уравнения представляет собой оценку значения целевой (зависимой) переменной.
Рассмотрим некоторые предположения, на которые опирается регрессионный анализ.
Предположение линейности, т.е. предполагается, что связь между рассматриваемыми переменными является линейной. Так, в рассматриваемом примере мы построили диаграмму рассеивания и смогли увидеть явную линейную связь.
Если же на диаграмме рассеивания переменных мы видим явное отсутствие линейной связи, т.е. присутствует нелинейная связь, следует использовать нелинейные методы анализа.
Предположение о нормальности остатков. Оно допускает, что распределение разницы предсказанных и наблюдаемых значений является нормальным. Для визуального определения характера распределения можно воспользоваться гистограммами остатков.
При использовании регрессионного анализа следует учитывать его основное ограничение. Оно состоит в том, что регрессионный анализ позволяет обнаружить лишь зависимости, а не связи, лежащие в основе этих зависимостей.
Регрессионный анализ дает возможность оценить степень связи между переменными путем вычисления предполагаемого значения переменной на основании нескольких известных значений.
Уравнение регрессии.
Уравнение регрессии выглядит следующим образом: Y=a+b*X
При помощи этого уравнения переменная Y выражается через константу a и угол наклона прямой (или угловой коэффициент) b, умноженный на значение переменной X. Константу a также называют свободным членом, а угловой коэффициент - коэффициентом регрессии или B-коэффициентом.
В большинстве случав (если не всегда) наблюдается определенный разброс наблюдений относительно регрессионной прямой.
Остаток - это отклонение отдельной точки (наблюдения) от линии регрессии (предсказанного значения).
Для решения задачи регрессионного анализа в MS Excel выбираем в меню Сервис "Пакет анализа" и инструмент анализа "Регрессия". Задаем входные интервалы X и Y. Входной интервал Y - это диапазон зависимых анализируемых данных, он должен включать один столбец. Входной интервал X - это диапазон независимых данных, которые необходимо проанализировать. Число входных диапазонов должно быть не больше 16.
На выходе процедуры в выходном диапазоне получаем отчет, приведенный в таблице 8.3а - 8.3в.
ВЫВОД ИТОГОВ
| Регрессионная статистика | |
| Множественный R | 0,998364 |
| R-квадрат | 0,99673 |
| Нормированный R-квадрат | 0,996321 |
| Стандартная ошибка | 0,42405 |
| Наблюдения | 10 |
Величина R-квадрат, называемая также мерой определенности, характеризует качество полученной регрессионной прямой. Это качество выражается степенью соответствия между исходными данными и регрессионной моделью (расчетными данными). Мера определенности всегда находится в пределах интервала [0;1].
В большинстве случаев значение R-квадрат находится между этими значениями, называемыми экстремальными, т.е. между нулем и единицей.
Если значение R-квадрата близко к единице, это означает, что построенная модель объясняет почти всю изменчивость соответствующих переменных. И наоборот, значение R-квадрата, близкое к нулю, означает плохое качество построенной модели.
В нашем примере мера определенности равна 0,99673, что говорит об очень хорошей подгонке регрессионной прямой к исходным данным.
множественный R - коэффициент множественной корреляции R - выражает степень зависимости независимых переменных (X) и зависимой переменной (Y).
Множественный R равен квадратному корню из коэффициента детерминации, эта величина принимает значения в интервале от нуля до единицы.
В простом линейном регрессионном анализе множественный R равен коэффициенту корреляции Пирсона. Действительно, множественный R в нашем случае равен коэффициенту корреляции Пирсона из предыдущего примера (0,998364).
| Коэффициенты | Стандартная ошибка | t-статистика | |
| Y-пересечение | 2,694545455 | 0,33176878 | 8,121757129 |
| Переменная X 1 | 2,305454545 | 0,04668634 | 49,38177965 |
| * Приведен усеченный вариант расчетов | |||
Исходя из расчетов, можем записать уравнение регрессии таким образом:
Y= x*2,305454545+2,694545455Направление связи между переменными определяется на основании знаков (отрицательный или положительный) коэффициентов регрессии (коэффициента b).
Если знак при коэффициенте регрессии - положительный, связь зависимой переменной с независимой будет положительной.
В нашем случае знак коэффициента регрессии положительный, следовательно, связь также является положительной.
Если знак при коэффициенте регрессии - отрицательный, связь зависимой переменной с независимой является отрицательной (обратной).
В таблице 8.3в. представлены результаты вывода остатков. Для того чтобы эти результаты появились в отчете, необходимо при запуске инструмента "Регрессия" активировать чекбокс "Остатки".
ВЫВОД ОСТАТКА
| 1 | 9,610909091 | -0,610909091 | -1,528044662 |
| 2 | 7,305454545 | -0,305454545 | -0,764022331 |
| 3 | 11,91636364 | 0,083636364 | 0,209196591 |
| 4 | 14,22181818 | 0,778181818 | 1,946437843 |
| 5 | 16,52727273 | 0,472727273 | 1,182415512 |
| 6 | 18,83272727 | 0,167272727 | 0,418393181 |
| 7 | 21,13818182 | -0,138181818 | -0,34562915 |
| 8 | 23,44363636 | -0,043636364 | -0,109146047 |
| 9 | 25,74909091 | -0,149090909 | -0,372915662 |
| 10 | 28,05454545 | -0,254545455 | -0,636685276 |
Следует учитывать, что рассматриваемый пример является достаточно простым и далеко не всегда возможно качественное построение регрессионной прямой линейного вида.
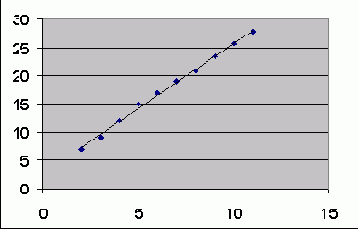
Рис. 8.3. Исходные данные и линия регрессии
Осталась нерассмотренной задача оценки неизвестных будущих значений зависимой переменной на основании известных значений независимой переменной, т.е. задача прогнозирования.
Имея уравнение регрессии, задача прогнозирования сводится к решению уравнения Y= x*2,305454545+2,694545455 с известными значениями x. Результаты прогнозирования зависимой переменной Y на шесть шагов вперед представлены в таблице 8.4.
| 11 | 28,05455 |
| 12 | 30,36 |
| 13 | 32,66545 |
| 14 | 34,97091 |
| 15 | 37,27636 |
| 16 | 39,58182 |
- построили уравнение регрессии;
- установили форму зависимости и направление связи между переменными - положительная линейная регрессия, которая выражается в равномерном росте функции;
- установили направление связи между переменными;
- оценили качество полученной регрессионной прямой;
- смогли увидеть отклонения расчетных данных от данных исходного набора;
- предсказали будущие значения зависимой переменной.
Прогнозные значения, полученные таким способом, являются средними значениями, которые можно ожидать.